Solutions for Midterm #1 Exam preparation exercises

Econ 301 - Haworth

 

 

1.  Suppose the government is concerned about gas shortages and so places a quota on gas purchases.  Before the quota, consumers are able to purchase as much as 12 gallons of gas per week.  The quota reduces this amount to no more than 10 gallons per week.  How are (typical) consumers affected by this quota?

 

There are two ways to analyze this problem.  The first involves the use of a market demand and supply graph.  If a quota is placed on gasoline, then the quota will ultimately affect the shape of the supply curve.  In other words, a quota restricts the ability of firms to supply a good.  Here is what the graph would look like.

 

For individual consumers, the blue line (S2) represents what the Supply curve facing them would look like after the quota.  Prior to the quota, the Supply curve is S1.  Their individual demand curve is depicted as D.

 

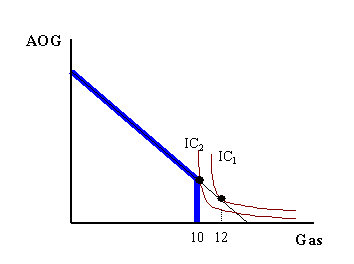
If we analyze this quota using an indifference curve graph, the result is similar.  Because the quota limits consumption of gas, from 12 gallons of gas to 10 gallons, we know where the typical consumer’s indifference curve is tangent to their budget constraint.  The graph below shows a possible result.

 

The blue line represents the new budget constraint, after the quota, which limits gas consumption to 10 gallons.  Consumers were previously consuming on the old budget constraint with indifference curve IC1.  After the quota, the consumer must move to the new budget constraint and indifference curve IC2.  Because IC2 is lower than IC1, IC2 yields a lower level of utility than IC1.  The quota makes this consumer worse off.

 

 

2.  After June 1st, Louisville-area (Jefferson County) gas stations are required to sell reformulated gasoline, which is about 20 cents more expensive than non-reformulated gas.  Gas stations in neighboring Oldham, Shelby and Bullitt Counties are not required to sell this gas.  How does this regulation affect consumers who live on the border of Jefferson and Shelby County?

 

Note here that the gas sold in these different locations represent two goods which are close substitutes for people living on the border of these two counties.  This implies that the indifference curves associated with buying gas in Jefferson and Shelby County are linear or nearly linear.  We can assume that the price of gas in the two counties was the same until June 1st, when the price of gas in Jefferson County increased.  This tells us that the slope of the budget constraint is nearly one before June 1st and greater than one afterwards (if Shelby County gas is on the vertical axis of our graph).

 

The graphs above illustrate the before and after cases for this situation.  The left side graph shows what is possible before the price increase.  The black budget constraint intersects the vertical and horizontal axis at points A and B resp.  There are two possible indifference curves placed on the graph, each representing a possible scenario.  The blue curve represents a consumer who buys Jefferson County gas before the price change, and the red curve represents someone who buys Shelby County gas before the price change.  Either is possible.

 

When prices rise in Jefferson County (after June 1), the budget constraint shifts inward.  The red curve remains where it was before the price change, but the blue curve changes.  The dotted blue curve is the represents the “pre-price change” indifference curve, while the solid blue curve is the “post-price change” indifference curve.  Similarly for the black budget constraint.  The price change forces this (blue) consumer to consume on a lower indifference curve and shifts their consumption to Shelby County gas.

 

 

3.  Assume that a local politician is running for office.  To appease soccer Moms (an important voting block), this politician creates a program for Louisville-area soccer Moms, allowing them to receive a monthly gas voucher that’s good for 20 gallons of gas.  Assume further that soccer Moms receive about $200 in monthly income, that gas prices are $2 per gallon and that a price index for “all other goods” is equal to $4.  Consider the following two groups of soccer Moms (let G = quantity of gas and A = quantity of all other goods).

 

Soccer Moms in group 1 have this utility function: 

(their MRSGA = -A/G)

 

Soccer Moms in group 2 have this utility function: 

(their MRSGA = -A/(9G))

 

 

Does the 40 gallon voucher make both of these groups better off?

 

The budget constraint facing both groups is 2G + 4A = 200.  We can rearrange this equation to be  A = -0.5G + 50.  Note that after plugging in the prices, the price ratio (PG/PA) is 0.5.

 

The effect on group 1:                                             The effect on group 2:

Solve MRSGA = -PG/PA for A                                 Solve MRSGA = -PG/PA for A

-A/G = -0.5                                                           -A/(9G) = -0.5

A = G/2                                                                 A = 9G/2

 

Plug into the BC and find G*                                   Plug into the BC and find G*

2G + 4(G/2) = 200                                                 2G + 4(9G/2) = 200

4G = 200                                                               20G = 200

G* = 50                                                                 G* = 10

Plug G* into BC and find A*                                  Plug G* into BC and find A*

2(50) + 4A = 200                                                  2(10) + 4A = 200

A* = 25                                                                 A* = 45

 

Overall, if group 1 could consume 50 gallons of gas and 25 units of all other goods, then their utility would be about 35.4.  Group 2 would have utility of about 38.7.

 

Now, we can determine how these groups are affected by the voucher program.  Note that these vouchers are comparable to giving Soccer Moms a $40 increase in their income.  That is, the budget constraint shifts out parallel, except that there is a “kink” at 20 gallons because this is the least amount of gas that a Soccer Mom will buy (due to the voucher program).  We can work with a “new” budget constraint, but we’ll assume that this program simply increases income by $40 and then account for the kink (later on).

 

The effect on group 1:                                             The effect on group 2:

Plug into the “new” BC and find G*                        Plug into the “new” BC and find G*

2G + 4(G/2) = 240                                                 2G + 4(9G/2) = 240

4G = 240                                                               20G = 240

G* = 60                                                                 G* = 12

(A* = 30)                                                               (A* = 54)

 

Overall, if group 1 could consume 60 gallons of gas and 30 units of all other goods, then their utility would be about 42.4.  Group 2 would have utility of about 46.5.

 

Note that group 1 locates at a point above the “kink” because their gas consumption exceeds 20 gallons (the minimum amount).  Group 2 does not locate above the “kink”, however, because they would consume only 12 gallons if this were actually a $40 increase in income.  That is, group 2 will have to locate on a lower indifference curve than that found above and correspondingly achieve a lesser amount of utility.  Because group 2 is “forced” to consume 20 gallons of gas, they will purchase 50 units of all other goods.  This yields utility of about 45.6.

 

Both groups are better off, but group 2 would be still better off if they simply received an additional $40 in income (rather than gas vouchers worth $40).