Barry Haworth
Department of Economics
University of Louisville
Economics 301
If youíve ever watched the game show "Who Wants to be a
Millionaire?" youíll notice that some players are willing to
guess at the answers to certain questions, while other players are
not. This handout seeks to better understand how economic agents
make choices under conditions of uncertainty within the context of
the Millionaire show. If youíre not familiar with the show, then
visit their
web site
or click here.
This handout seeks to answer the question of why a player would be willing to guess and risk losing a certain amount of money. Letís first consider what happens after a player answers the $32,000 question correctly. If you watch the show, then youíll notice that players never pass on the $64,000 question, even when a player doesnít know the answer to that question. Why is this?
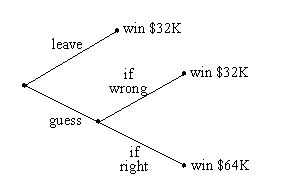
After answering the $32,000 question correctly, players face one of the three possible outcomes given in the tree below:

Clearly, even when the player doesnít know the answer to the $64,000 question, a dominant strategy involves at least guessing because by doing so, a player can become no worse off than by simply ending the game (and leaving with the minimum prize of $32,000). In addition, there is a possibility that the player can guess correctly and become better off as long as the probability of guessing correctly is greater than zero.
Assume that the player has correctly guessed the answer to the $64,000 question.
Now, we observe that when faced with a ($125,000) question, very few players are
willing to guess if they donít know the answer to this question. Why?
Letís assume that each player derives positive utility from their winnings. It is reasonable to assume that this utility increases with winnings, but at a decreasing rate. If so, then players possess diminishing marginal utility with respect to their earnings, which allows us to characterize them as risk averse. Risk aversion is defined as an unwillingness to play a fair game. Fair games are those games with an expected value of zero. What is the expected value associated with guessing at the answer to the $125,000 question?
There are four possible answers, so the probability of guessing correctly (incorrectly) is 0.25 (0.75). If correct, then the player wins an additional $61,000. If incorrect, then the player loses $32,000. Therefore, the expected v alue associated with guessing is:
If a risk averse player is unwilling to play games with expected values of zero, then a risk averse player would never guess at the $125,000 question if guessing implied an expected loss of $8,750. Some players do guess, however, so what about them? A person is risk loving if they are willing to play a fair game. Players who guess at the $125,000 would then have to be extremely risk loving.
When considering whether to guess at the $125,000 question, a player may
have lifelines remaining. If so, then it is a good idea to use them. Suppose a
player decides to use the 50:50 lifeline, which decreases (increases) the
probability of being incorrect (correct) from 0.75 to 0.5 (0.25 to 0.5). Would a
risk averse player be willing to guess now?
First, letís consider the expected value of this guess.
An expected gain of $14,500 dictates that this is a more than fair game, but the decision of whether to guess here ultimately depends upon the expected utility associated with this guess. Consider two possible players and their respective utility functions (where E = earnings or income):
| Player A | Player B |
| UA(E) = (E)0.5 | UB(E) = 100(E)0.05 |
After using the 50:50 lifeline, the expected utility associated with guessing becomes (where E1 = income if guess wrong, E2 = income if guess right):
| Player A | Player B |
| EUA = (0.5)(UA(E1)) + (0.5)(UA(E2)) | EUB = (0.5)(UB(E1)) + (0.5)(UB(E2)) |
| EUA = (0.5)($32K)0.5 + (0.5)($125K)0.5 | EUB = (0.5)(100)($32K)0.05 + (0.5)(100)($125K)0.05 |
| EUA = 266.219 | EUB = 173.902 |
Both players derive positive (expected) utility from a 50:50 guess at the $125,000 question. The decision of whether to guess, however, depends on whether the expected utility of guessing is greater or less than the (certain) utility associated with ending the game and walking away with $64,000. For each player, weíll express this as expected utility, where the probability of winning $64,000 is 100%:
| Player A | Player B |
| EUA = (1.0)($64K)0.5 | EUB = (1.0)(100)($64K)0.05 |
| EUA = 252.982 | EUB = 173.904 |
Comparing the results for each player, we see that Player A derives greater expected utility from guessing at this question, whereas Player B derives greater utility from not guessing.
Itís possible to observe this result graphically. A (concave) utility function
for each player is depicted below. Player A (left) and Player B (right) can both derive
U1 utility from simply ending the game and taking the $64,000.
The expected utility of guessing at the $125,000 question (after using
the 50:50) depends on the expected value of that guess. For both players,
the expected value of their income associated with guessing is given as $72500.
A red dotted line connects the outcomes associated with being correct (i.e.
winning $125K) and being incorrect (i.e. winning $32K). This line represents
the average utility associated with these two outcomes (geometrically, any line
segments connecting two points on a curve represents the average value of those
points). At the intersection of the dotted line representing the expected value
of guessing (i.e. the dotted line coming up from $72.5K) and the red dotted line
we find the expected utility associated with guessing. On each graph, this is
represented by the purple dotted line leading to U2.
Note that for Player A, U2 > U1, and for Player B,
U2 < U1. This is the same result we derived above
using the utility functions for each player. Consequently, after using the
50:50, Player A will want to guess at the $125,000 question, while Player B will
not want to guess (prefering instead to go home with a certain $64,000).