Let’s call the amount demanded (supplied) the quantity demanded (quantity supplied). Defined this way, we have a relationship between a good’s price and the good’s quantity demanded (supplied). Of course, there are many other variables which may influence the quantity demanded or quantity supplied, but we'll get into that elsewhere. For now, we assume that price and quantity are related and that nothing else changes in such a way as to disturb the relationship between price and quantity.

From our definitions above, we can now derive a set of possible points which involve a potential price being charged and the quantity which corresponds with that price. The next step in our formalization is to determine what the relationship is between price and quantity demanded, as well as price and the quantity supplied. Once this is done, we can put that information on a graph. Our graph will ultimately contain a pair of curves one curve for each set of points - the set of points for price and quantity demanded, which yields a demand curve, and the set of points for price and quantity supplied, which gives us a supply curve.

We begin our discussion of demand and supply then by first developing the demand curve relationship, followed by the supply curve relationship. After doing that, we put the curves together and ask about the actual market price and quantity that would arise in this setting.

Demand. If the price of something falls (rises), and nothing else changes during that time, then demanders will most likely purchase more (less) of that good. We know this because if someone gains less from buying a particular unit of some good than what they give up to get it, then that someone won’t buy as much of the good. This implies an inverse relationship between prices and the quantity demanded of something.

For example, suppose there’s a good that when the good’s price is $100, zero units are sold, but for any price below $100, at least something is sold. Assume further that every time the price falls by $30, an additional 30 units are sold (i.e. a decrease or increase in the price is always equal to an increase or decrease, respectively, in the quantity demanded). We can graph this relationship as:

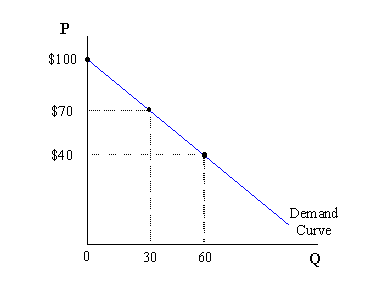
As the graph reveals, this information leads to a demand curve for the good in question. The curve’s negative slope gives evidence of what we call the Law of Demand (i.e. increases in price lead to decreases in quantity, and vice versa).

Supply. If the price of something falls (rises), and nothing else changes during that time, then suppliers will most likely produce less (more) of that good. Prices provide the incentive for suppliers to produce. Lower prices lead to the supplier receiving less benefit from each unit sold. As a result, suppliers produce fewer units when prices fall. This implies a positive relationship on the supply side of prices and quantities.

Now, consider this supply-related example. Using the good discussed above, we can assume that as long as the price is above $10, some number of units are sold. Whenever the price rises by $30, an additional 15 units are produced (i.e. a decrease or increase in the price is always equal to half the decrease or increase, respectively, in the quantity supplied). This relationship appears as follows:

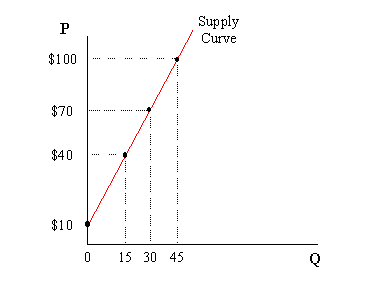
From this information, we obtain the supply curve illustrated in the graph above. The supply curve’s positive slope also allows us to see the Law of Supply (i.e. price and quantity change in the same direction).

Demand and Supply together. When the actions of both suppliers and demanders are accounted for, we have a market. Because markets involve exchange, the demand and supply curves allow us to predict the quantity and price that arise in this market during exchange.

Let’s assume that every unit for sale in a particular market is identical. If a demander is willing to pay a price for a certain quantity of units and that price is acceptable to suppliers, then the demander should be able to purchase those units. Similarly, if the supplier asks for a price that is acceptable to demanders, then all units produced should be sold (i.e. the supplier won’t produce more than is necessary). This implies that, at the market price, the quantity demanded will equal the quantity supplied. There will be no shortage and no surplus if demanders and suppliers can agree upon a market-clearing price.

What price arises then? In the graph below, the demand and supply curves unite to find this price. The only possible point where we can achieve the agreement between suppliers and demanders that was just discussed occurs where the price is $70. At $70, demanders ask for 30 units and suppliers are willing to provide 30 units. At any other price, either more quantity will be demanded than supplied, or more quantity will be supplied than demanded.

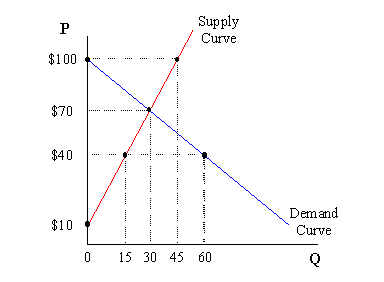
If we consider the price of $70 more closely, then we also note that demanders and suppliers have no reason to "move away" from this price. If they were to agree on a higher price, then suppliers will produce too much and a surplus will result. If the price falls from $70, then a shortage occurs. Consequently, the price of $70 is called an equilibrium price because equilibrium implies a sense of balance. Similarly, the quantity of 30 is the equilibrium quantity. On a graph, or when we work with algebra, these equilibrium values are denoted as P* and Q* respectively.